УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

УЗБЕКСКОЕ АГЕНТСТВО СВЯЗИ И ИНФОРМАТИЗАЦИИ

ТАШКЕНТСКИЙ УНИВЕРСИТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

ФАКУЛЬТЕТ ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ

ПРОЕКТИРОВАНИЕ СИСТЕМ РЕАЛЬНОГО ВРЕМЕНИ

Mетодические указания по выполнению лабораторных работ

Ташкент 2012

Авторы: Х. Н. Зайнидинов, С.А. Жовлиев, С.Э. Отто

«Проектирование систем реального времени», ТУИТ, 59 с., Ташкент 2012.

Методические указания по выполнению лабораторных работ по дисциплине «Проектирование систем реального времени» для студентов магистратуры специальности 5А330204- Информационные системы (по отраслям).

Методические указания будет полезным пособием для аспирантов и преподавателей, кто интересуется исследованием и проектированием систем реального времени в различных отраслях.

Рецензенты:

зав. кафедрой «Компьютерные системы» Ташкентского университета информационных технологий

д.т.н., профессор Мусаев М.М.

д.т.н., профессор, в.н.с.

Института математики и

информатики, АН РУз Исмаилов М.А.

Содержание

1.	Введение ………………………………………………………...	4
2.	Основы Matlab…………………………………………………..	5
3.	Простые вычисления и визуализация результатов в среде Matlab…………………………………………………………….	15
4.	Многомерные вычисления и визуализация результатов в среде Matlab…………………………………………………….	21
5.	Моделирование устройства с помощью Simulink…………….	30
6.	Моделирование аналогового сигнала в Matlab и Simulink…..	40
7.	Моделирование специализированного процессора обработки сигналов на основе кубических базисных сплайнов с использованием возможностей среды Matlab и Simulink……	51
8.	Литература	58

Введение

В настоящее время в документах и публикациях с различной тематикой встречаются слова о требовании, поддержке и т.д. «работы в режиме реального времени», «режима реального времени». Толковый словарь по вычислительным системам дает такое определение: «Любая система, в которой существенную роль играет время генерации выходного сигнала. Это обычно связано с тем, что входной сигнал соответствует каким-то изменениям в физическом процессе, и выходной сигнал должен быть связан с этими же изменениями. Временная задержка от получения входного сигнала до выдачи выходного сигнала должна быть небольшой, чтобы обеспечить приемлемое время реакции». Время реакции является системной характеристикой: при управлении ракетой требуется реакция в течении нескольких миллисекунд, тогда как для диспетчерского управления движением пароходов требуется время реакции, измеряемое днями. Системы обычно считаются системами реального времени, если время их реакции имеет порядок миллисекунд; диалоговыми считаются системы с временем реакции порядка нескольких секунд, а в системах пакетной обработки время реакции измеряется часами или днями. Примерами систем реального времени являются системы управления физическими процессами с применением вычислительных машин, системы торговых автоматов, автоматизированные системы контроля и автоматизированные испытательные комплексы.

Данные методические указания предназначены для изучения методов моделирования, основных способов программирования и проектирования систем реального времени с использованием системы Matlab и входящего в него пакета моделирования Simulink.

Лабораторный цикл содержит следующих работ:

1. Основы Matlab.

2. Простые вычисления и визуализация результатов в среде Matlab.

3. Многомерные вычисления и визуализация результатов в среде Matlab.

4. Моделирование устройства с помощью Simulink.

5. Моделирование аналогового сигнала в Matlab и Simulink

6. Моделирование специализированного процессора обработки сигналов на основе кубических базисных сплайнов с использованием возможностей среды Matlab и Simulink.

Содержание отчета по каждой работе:

1. Название работы, задание в соответствии с вариантом.

2. Теоретическая часть.

3. Программа.

4. Результаты выполнения программы на ПК.

5. Выводы.

Лабораторная работа №1.

Основы Matlab.

Цель работы:

По указанной литературе изучить:

- основы системы Matlab,

- системное меню Matlab,

- основы работы с демонстрационными примерами,

- основные системные команды,

- правила ввода команд и данных,

- правила вывода результатов.

Теоретическая часть.

1. Работа в среде Mathlab

Система MATLAB в настоящее время является мощным и универсальным средством решения задач, возникающих в различных областях человеческой деятельности. Спектр проблем, решение которых может быть осуществлено при помощи MATLAB, охватывает: матричный анализ, обработку сигналов и изображений, задачи математической физики, оптимизационные задачи, обработку и визуализацию данных, нейронные сети, нечеткую логику и многие другие.

1.1. Работа с командным окном (в режиме калькулятора)

При запуске MATLAB на экране появляется командное окно MATLAB Command Window:

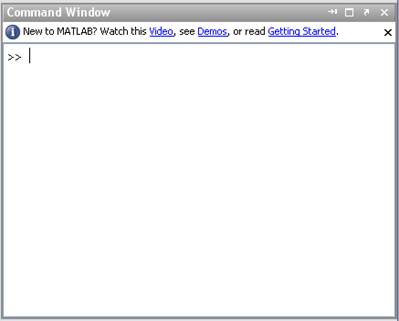
Рис. 1.1. Командное окно системы.

Символ >> означает приглашение командной строки к вводу команды.

Набор любой команды или выражения должен сопровождаться нажатием клавиши <Enter> для того, чтобы система MATLAB выполнила введенную команду или вычислила выражение.

Встроенные математические функции MATLAB позволяют находить значения различных выражений. Команды для вычисления выражений имеют вид, свойственный всем языкам программирования высокого уровня. Полный перечень встроенных математических функций можно найти в справочной системе MATLAB.

1.2. Правила ввода комментариев

Основным комментарием является первая строка текстовых комментариев, а дополнительным — последующие строки. Основной комментарий выводится при выполнении команд lookfor и help имя_каталога. Полный комментарий выводится при выполнении команды help Имя_файла. Рассмотрим следующий файл-сценарий:

%Plot with color red

%Строит график синусоиды линией красного цвета

%с выведенной масштабной сеткой в интервале [xmin.xmax]

x=xmin:0.1:xmax;

plot(x.sin(x).'r')

grid on

Первые три строки здесь — это комментарий, остальные — тело файла. Обратите внимание на возможность задания комментария на русском языке. Знак % в комментариях должен начинаться с первой позиции строки. В противном случае команда help name не будет воспринимать комментарий (иногда это может понадобиться) и возвратит сообщение вида No help comments found in-name.m.

1.3. Работа с панелью инструментов

Панель инструментов (рис. 1) дает наиболее простой и удобный (особенно для начинающих пользователей) способ работы с системой MATLAB. При этом основные команды вводятся указанием курсором мыши на нужную кнопку с нажатием левой клавиши мыши. Кнопки имеют изображение, явно подсказывающее их назначение.

Рис.1.2. Панель инструментов системы

Прежде всего перечислим назначение всех кнопок панели инструментов:

· New M-file (Новый m-файл) — выводит пустое окно редактора m-файлов;

· Open file (Открыть файл) — открывает окно для загрузки m-файла;

· Cut (Вырезать)— вырезает выделенный фрагмент и помещает его в буфер;

· Сору (Копировать)— копирует выделенный фрагмент в буфер;
Paste (Вставить)— переносит фрагмент из буфера в текущую строку ВВОДА

· Undo (Отменить)— отменяет предшествующую операцию;

· Redo (Повторить) — восстанавливает последнюю отмененную операцию;

· Simulink — открывает окно браузера библиотек Simulink;

· Help (Помощь)— открывает окно справки.

1.4. Меню системы

Перейдем к описанию основного меню системы MATLAB 6.0. Это меню содержит всего шесть пунктов:

- File — работа с файлами;

- Edit — редактирование сессии;

- View — вывод и скрытие панели инструментов;

- Web — доступ к Интернет-ресурсам;

- Windows — установка Windows-свойств окна;

- Help — доступ к справочным подсистемам.

Подменю File

Подменю File содержит ряд операций и команд для работы с файлами и содержит следующие операции:

- New - открывает подменю с позициями:

- M-file — открытие окна редактора/отладчика m-файлов;

- Figure — открытие пустого окна графики;

- Model — открытие пустого окна для создания Simulink-модели;

- GUI — открытие окна разработки элементов графического интерфейса пользователя.

- Open — открывает окно загрузки файла.

- Close Command Windows — закрывает окно командного режима работы (оно при этом исчезает с экрана).

- Import data — открывает окно импорта файлов данных.

- Save Workspace As... — открывает окно записи рабочей области в виде файла с заданным именем.

- Set Path — открывает окно установки путей доступа файловой системы.

- Preferences... — открывает окно настройки элементов интерфейса.

- Print... — открывает окно печати всего текущего документа.

- Print Selection... — открывает окно печати выделенной части документа.

- Exit — завершает работу с системой.

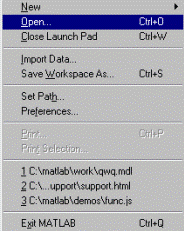
Рис. 1.3. Меню файловых операций File

Меню Edit содержит операции и команды редактирования, типичные для большинства приложений Windows:

- Undo (Отменить) — отмена результата предшествующей операции;

- Redo (Повторить) — отмена действия последней операции Undo;

- Cut (Вырезать) — вырезание выделенного фрагмента и перенос его в буфер;

- Сору (Копировать) — копирование выделенного фрагмента в буфер;

- О Paste (Вставить) — вставка фрагмента из буфера в текущую позицию курсора;

- Clear (Очистить) — операция очистки выделенной области;

- Select All (Выделить) — выделение всей сессии;

- Delete (Стереть) — уничтожение выделенного объекта;

- Clear Command Windows (Очистить командное окно) — очистка текста сессии (с сохранением созданных объектов);

- Clear Command History (Очистить окно истории команд) — очистка окна истории;

- О Clear Workspace — очистка окна браузера рабочей области.

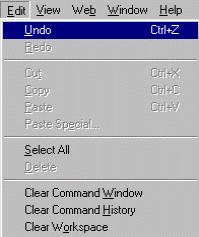
Рис. 1.4. Меню Edit.

Команда Clear Command Window очищает окно командного режима работы и помещает курсор в верхний левый угол окна. Однако все определения, сделанные в течение стертых таким образом сессий, сохраняются в памяти компьютера. Для очистки экрана используется также команда clc, вводимая в командном режиме.

Меню View и Window

В MATLAB 6.Х набор команд меню View существенно расширен, и теперь с помощью этого меню можно существенно менять вид пользовательского интерфейса.

Меню Window активно только в случае, если в систему загружены файлы. При этом оно имеет единственную команду Close All (закрыть все окна) и открывающийся список всех загруженных файлов. Он позволяет выбрать окно указанного пользователем файла и сделать его открытым.

1.5. История команд

Содержит историю команд по времени, а также историю всех операций, выполняемых в командном окне.

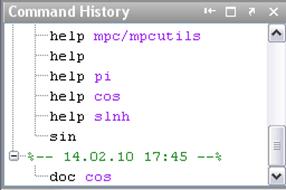
Рис.1.5. Окно истории команд

2. Работа с демонстрационными примерами

2.1. Вызов списка демонстрационных примеров

Одним из самых эффективных методов знакомства со сложными математическими системами является ознакомление со встроенными примерами их применения.

Система MATLAB содержит многие сотни таких примеров — практически по примеру на каждый оператор или функцию.

Наиболее поучительные примеры можно найти в разделе demos, исполнив команду

» help demos

Вызов галереи демонстраций

В меню Help имеется команда Demos, дающая доступ к галерее демонстрационных примеров применения системы MATLAB. При запуске этой команды появляется окно демонстрационных примеров MATLAB Demos, показанное на рисунке:

Рис.1.6. Окно демонстрационных примеров

Это же окно можно вызвать выполнением команды demo в режиме диалога.

В этом окне имеются три панели:

· левая панель с перечнем разделов, по которым предлагаются примеры;

· панель с описанием выбранного раздела примеров;

· панель с перечнем примеров по выбранному разделу.

Выбрав раздел примеров (щелчком мыши), затем следует выбрать нужный пример. После этого нажатием кнопки Run можно запустить m-файл с выбранным примером и наблюдать результат его работы.

Окно MATLAB Demos дает возможность ознакомиться со многими десятками самых серьезных примеров применения системы MATLAB и позволяет убедиться в высоком качестве визуализации их решений. При необходимости всегда можно ознакомиться с файлом любого примера и использовать его для решения схожих задач.

2.2. Копирование демонстрационных примеров

Вполне возможно, что вы захотите воспользоваться каким-либо примером для своих целей. Для этого можно использовать m-файл примера или перенести его текст в командное окно MATLAB, используя буфер обмена. Покажем, как это делается. В нижней части окна примера показано, каким образом осуществляется копирование примера: текст примера выделяется мышью и используется команда Сору (Копировать) меню Edit окна примера, в результате чего текст примера попадет в буфер обмена.

После этого надо вернуться в командное окно MATLAB и, используя команду Paste (Вставить) меню Edit, перенести текст примера из буфера в текущую строку ввода. Выполнив команду (как обычно, клавишей Enter), можно наблюдать исполнение примера.

3. Операции в среде MATLAB.

3.1. Команды, операции и параметры

Открытая позиция строки меню содержит различные операции и команды. Выделенная команда или операция исполняется при нажатии клавиши Enter (Ввод). Выполнение команды можно также осуществить щелчком мыши или нажатием на клавиатуре клавиши, соответствующей выделенному символу в названии команды.

Между командами и операциями нет особых отличий, и в литературе по информатике их часто путают. Мы будем считать командой действие, которое исполняется немедленно. А операцией — действие, которое требует определенной подготовки, например открытие окна для установки определенных параметров.

Параметр (option)— это значение определенной величины, действующее во время текущей сессии. Параметрами обычно являются указания на применяемые наборы шрифтов, размеры окна, цвет фона и т. д.

Арифметические операторы являются самыми распространенными и известными. В отличие от большинства языков программирования в системе MATLAB практически все операторы являются матричными, т. е. предназначены для выполнения операций над матрицами. В табл. приводится список арифметических операторов и синтаксис их применения.

Арифметические операторы и функции MATLAB

Функция	Название Оператор	Синтаксис
Plus	Плюс +	М1+М2
Uplus	Унарный плюс +	+М
Minus	Минус	М1-М2
Uminus	Унарный минус	-М
Mtimes	Матричное умножение *	М1*М2
Times	Поэлементное умножение массивов .*	А1*А2
Mpower	Возведение матрицы в степень	М1^х
Power	Поэлементное возведение массива в степень	А1^х
Mldivide	Обратное (справа налево) деление матриц \	M1\M2
Mrdivide	Деление матриц слева направо /	М1/М2
Ldivide	Поэлементное деление массивов справа налево . \	А1.\А2
Rdivide	Поэлементное деление массивов слева направо . /	А1 . /А2
Kron	Тензорное умножение Кронекера kron	kron(X.Y)

Каждый оператор имеет аналогичную по назначению функцию. Например, оператору матричного умножения * соответствует функция mtimes(Ml,M2).

В-А -> minus (В. А)

А. ^{^}2 -> power(A,2)

Соответствие функций операторам и командам в системе MATLAB является одним из основных положений программирования. Оно позволяет одновременно использовать элементы как операторного, так и функционального программирования.

Следует отметить, что в математических выражениях операторы имеют определенный приоритет исполнения. Например, в MATLAB приоритет логических операторов выше, чем арифметических, приоритет возведения в степень выше приоритетов умножения и деления, приоритет умножения и деления выше приоритета сложения и вычитания. Для изменения приоритета операций в математических выражениях используются круглые скобки. Степень вложения скобок не ограничивается.

Задание к работе

Задача 1. Изучить интерфейс Matlab.

Задача 2. Ознакомиться с демонстрационными примерами Matlab.

Задача 3. Выполнить в режиме калькулятора следующие действия:

1. Ввод исходных операндов.

2. Выполнить над операндами 1 и 2 операцию 1.

3. Выполнить над результатом и операндом 1 операцию 2.

4. Выполнить над результатом предыдущего действия и операндом 2 операцию 3.

5. Возвести почленно операнд 1 в степень 3.

Варианты заданий

№	Операнд 1	Операнд 2	Операторы
№	Операнд 1	Операнд 2	1	2	3
1	V=[12 34 61 45 11]	v = 34	*	./	+
2	V=[80 67 34 11 45]	v = 43	/	.*	-
3	V=[19 77 45 11 67]	v = -5	+	.\	/
4	V=[11 98 67 45 22]	v = 7	-	.*	/
5	V=[67 34 67 45 56]	v = -12	+	.\	*
6	V=[18 36 45 45 4 ]	v = 10	/	./	-
7	V=[55 43 8 45 23]	v = 44	/	.*	/
8	V=[32 28 55 45 34]	v = 87	*	-	/
9	V=[14 34 33 45 15]	v = 78	*	+	+
10	V=[15 23 17 45 9]	v = -22	/	-	*
11	V=[10 34 10 45 7]	v = -14	*	-	*
12	V=[95 56 5 45 54]	v = 99	+	./	+
13	V=[18 90 35 45 46]	v = 32	*	.*	-
14	V=[24 34 87 45 88]	v = -43	/	.*	/
15	V=[14 41 90 45 77]	v = 55	/	+	+

Методические указания:

1. В Matlab все данные рассматриваются, как матрицы. Тип результатов определяется автоматически по виду выражения.

2. В идентификаторах высота буквы имеет значение. Рекомендуется для имен простых переменных выбирать сточные буквы, а для структурированных (векторы и массивы) прописные.

3. Векторы вводятся в квадратных скобках, компоненты вектора разделяются пробелами. Например, V=[1 2 3 4].

4. Матрицы вводятся в квадратных скобках, внутри которых размещаются векторы строк, разделенные знаком точка с запятой (;). Например V=[1 2 3;2 6 5;9 1 3].

5. Если данные не умещаются в строке, строку можно отобразить в нескольких строках, используя разделить в виде многоточия (не менее трех точек).

6. Значение π задается системной константой с именем pi.

7. В Matlab возможны два режима работы:

- В командном окне, как с калькулятором. В этом случае каждое действие сразу же исполняется.

- В редакторе программ. В этом случае программа вводится, как обычно, а исполняется по команде встроенного отладчика.

8. При работе в режиме калькулятора выражения могут вводится:

- В прямой форме, тогда после завершения ввода ответ будет выведен под встроенным системным именем ans. Переменная с этим именем всегда хранит результат последнего вычисления.

- В форме оператора присвоения, когда переменной с выбранным именем присваивается значение выражения. Ответ в этом случае выводиться под именем этой переменной.

- Любое уже определенное значение можно вызвать из рабочей области по имени переменной.

9. Если вычисляется значение переменной с выбранным именем по заданному выражению, результат выводится под именем этой переменной в следующей строке. Векторы выводятся в строке пробелами, матрицы – построчно, каждая содержит вектор строки.

10. При работе с программой неграфические результаты выводятся в окно командной строки. При необходимости их можно выводить, как текст, в специально создаваемое окно.

11. Вывод результата можно заблокировать, если в конце строки ввода ввести знак точка с запятой (;). Значение переменной, которой результат присваивается, храниться в рабочей области.

12. При работе с массивами определены операторы почленного выполнения. В них перед символом операции вводится (.).

13. Символ присвоения – знак равенства (=). Равенство, как оператор отношения в условиях, вводится, как двойное равенство (==).

Контрольные вопросы

1. Структура окна системы Matlab.

2. Команды пункта “File” системного меню.

3. Команды пункта “Edit” системного меню.

4. Команды пункта “View” системного меню.

5. Команды пункта “Web” системного меню.

6. Команды пункта “Window” системного меню.

7. Правила работы с демонстрационными примерами.

8. Правила ввода команд.

9. Правила ввода функций и операндов.

10. Правила ввода выражений.

11. Правила ввода комментариев.

12. Просмотр результатов операций.

Лабораторная работа № 2

Простые вычисления и визуализация результатов в среде Matlab

Цель работы:

1. По указанной литературе изучить:

- системное меню редактора Matlab,

- основные системные команды,

- ранжированные переменные,

- правила вывода результатов,

- правила вывода результатов в виде двумерных графиков,

- правила отладки программ.

2. Разработать алгоритмы решения задач из варианта задания.

3. Составить программы решения задач.

Теоретическая часть.

1. Работа в режиме редактирования и отладки m-файлов

Интерфейс редактора/отладчика m-файлов Для подготовки, редактирования и отладки m-файлов служит специальный многооконный редактор. Он выполнен как типичное приложение Windows. Редактор можно вызвать командой edit из командной строки или командой New > M-file из меню File. После этого в окне редактора можно создавать свой файл, пользоваться средствами его отладки и запуска. Перед запуском файла его необходимо записать на диск, используя команду Filе > Save as в меню редактора.

Рис. 2.1. Редактор/отладчик файлов при записи файла на диск

Подготовленный текст файла надо записать на диск. Для этого используется команда Save As, окно которой видно на рисунке 9 внутри окна системы редактора/ отладчика. После записи файла на диск можно заметить, что команда Run в меню Tools (Инструменты) редактора становится активной (до записи файла на диск она пассивна) и позволяет произвести запуск файла.

На первый взгляд может показаться, что редактор/отладчик — просто лишнее звено в цепочке «пользователь — MATLAB». И в самом деле, текст файла можно было бы ввести в окно системы и получить тот же результат. Однако на деле редактор/отладчик выполняет важную роль. Он позволяет создать m-файл (программу) без той многочисленной «шелухи», которая сопровождает работу в командном режиме. Далее мы убедимся, что текст такого файла подвергается тщательной синтаксической проверке, в ходе которой выявляются и отсеиваются многие ошибки пользователя. Таким образом, редактор обеспечивает синтаксический контроль файла.

2. Файлы сценарии и файлы-функции

Есть два типа m-файлов: файлы-сценарии и файлы-функции. Важно, что в процессе своего создания они проходят синтаксический контроль с помощью встроенного в систему MATLAB редактора/отладчика m-файлов.

Файл-сценарий, именуемый также Script-файлом, является просто записью серии команд без входных и выходных параметров.

Свойства файлов-сценариев:

· они не имеют входных и выходных аргументов;

· работают с данными из рабочей области;

· в процессе выполнения не компилируются;

· представляют собой зафиксированную в виде файла последовательность операций, полностью аналогичную той, что используется в сессии.

Для запуска файла-сценария из командной строки MATLAB достаточно указать его имя в этой строке.

Файл-функция отличается от файла-сценария прежде всего тем, что созданная им функция имеет входные параметры, список которых указывается в круглых скобках. Используемые в файле-функции переменные являются локальными переменными, изменение значений которых в теле функции никоим образом не влияет на значения, которые те же самые переменные могут иметь за пределами функции.

Задание к работе

Задача 1.

- Ввести текст в виде комментария, как заглавие программы.

- Ввести исходные данные.

- Задать изменение аргумента.

- Вычислить значения функций 1 и 2 для аргумента в заданном интервале.

- Вывести графики функций одновременно на одном графике в декартовых координатах. Для разных графиков использовать разный тип линий.

Задача 2.

- Пункты 1….4 задачи 1.

- Вывести графики функций в двух подокнах на одном графике. Графики сделать в столбиковом формате.

Варианты заданий

№	Функция 1	Функция 2	a	b	h
1	y = sin(x)	z = exp(x+3)/5000-1	-2π	2π	π/20
2	y = cos(x)	z = 0.00025e³-x-0.6	-2π	2π	π/20
3	y = \|tg(x)\|+0.1	z = (1+x)⁶	-2π	2π	π/20
4	y = (x²-1)/15	z = 1+ sin(x)	-2π	2π	π/20
5	y = (x³-2)/15	z = 5 cos(x)	-2π	2π	π/20
6	y = x²-10	z = 0.025exp(-1.2x)	-5	5	1
7	y = 3 sin(x)	z = 0.015x³	-5	5	1
8	y = 4 sin(x)	z = 0.05x²	1	10	1
9	y = 6 sin(x)	z = 0.01x³	-10	10	1
10	y = 2 + cos(x)	z = -0.05(x²+10cos(x))	-8	8	1
11	y = sin²(x/3)	z = 0.01(x²– 40sin(x))	-8	8	1
12	y = cos³(x)	z = sin(x) + sin(2x)	-π	π	π/8
13	y = 0.5x + cos²(x)	z = sin²(x) + cos(x)	-π	π	π/8
14	y = sin(x) + cos²(2x)	z = x(0.5+x)exp(0.1x)	-π	π	π/8
15	y = \|sin(x)\|exp(x/2)	z = 5x – x^1.5 + sin(x)	0	5	0.5

Методические указания

1. Текстовые пояснения в программу вводятся, как комментарий. Он начинается с символа %, который располагается в первой позиции строки. Комментарий это текст! В него не надо включать символы операций.

2. Для формирования XY графика необходимо:

- Задать аргумент в формате х=<нач. значение>:<шаг>:<конеч. значение>.

- Вычислить функцию, например, у=f(х).

- Вывести график процедурой plot(x,y,s). Процедура рисует график прямыми линиями между вычисленными точками. Здесь s – строковая константа, задающая параметры линии, ее можно пропускать. Определены следующие значения s:

Цвет линии		Тип точки		Тип линии
Y	желтый	.	точка	-	сплошная
M	фиолетовый	о	кружок	:	двойной пунктир
C	голубой	х	крест	-.	штрих пунктир
R	красный	+	плюс	--	штрих
G	зеленый	*	звездочка
B	синий	s	квадрат
W	белый	d	ромб
K	черный	v	треугольник вверх
		<	треугольник влево
		>	треугольник вправо
		p	пятиугольник
		h	шестиугольник

- Если на одном графике нужно отобразить несколько функций, например, у1=f(х) и у2=f(х)., то они вначале вычисляются, а затем выводятся процедурой plot(x,y1,′s1′,x,y2,′s2….), в которой в качестве параметров для каждой функции следуют группы <аргумент, функция, строка типа линии>.

- Для создания в графическом окне нескольких подокон для вывода графиков используется процедура subplot(m,n,p), где m - число подокон в окне по горизонтали, n – по вертикали, p – номер используемого подокна (нумерация с 1).

- Для формирования графика в столбиковой форме нужно использовать процедура bar(x,y). При выводе такого графика в подокно строка программы имеет вид subplot(m,n,p), bar(x,y).

Пример выполнения

Задание	Функция 1	у = 2sin(x)
	Функция 2	z = 0.02x³
	Начальное значение аргумента	a = -2π
	Конечное значение аргумента	b = 2π
	Шаг изменения аргумента	h = π/20

Задача 1

% Задача 1

% Диапазон и шаг

a= -2*pi

b= 2*pi

h= pi/20

% Задание аргумента

Х=a:h:b;

% Расчет функций

Y= 2*sin(X);

Z= 0.02*X.^3;

% Вывод графиков с одинаковым типом линии в окно 1

figure(1);

plot(X,Y,X,Z);

% Включим координатную сетку

grid on

% Вывод графиков с разными типами линии в окно 2

figure(2);

plot(X,Y,′-′,X,Z,′:′);

% Включим координатную сетку

grid on

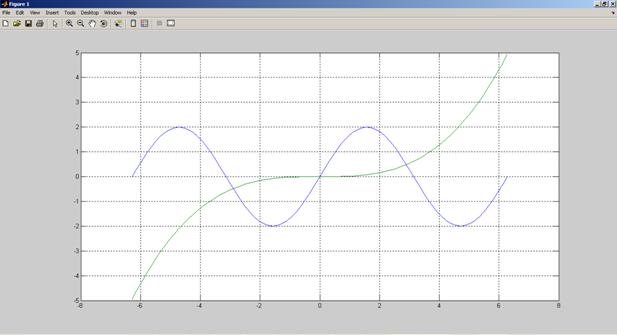
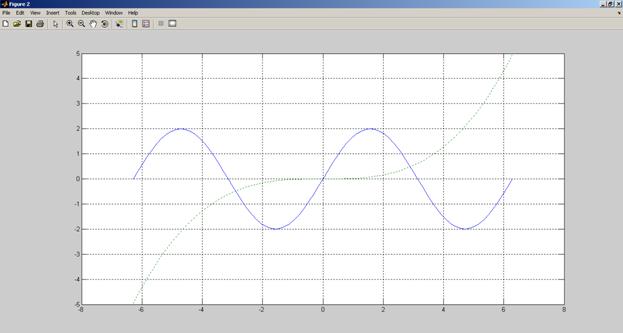
Рис. 2.2. Результат выполнения программы (задача 1)

Задача 2

% Задача 2

% Диапазон и шаг

a= -2*pi

b= 2*pi

h= pi/20

% Задание аргумента

Х=a:h:b;

% Расчет функций

Y= 2*sin(X);

Z= 0.02*X.^3;

% Вывод графика 1 в виде столбиков в подокно 1

subplot(2,1,1),bar(X,Y);

% Включим координатную сетку

grid on

% Вывод графика 2 в виде столбиков в подокно 2

subplot(2,1,2),bar(X,Z);

% Включим координатную сетку

grid on

Рис. 2.3. Результат выполнения программы (задача 2)

Контрольные вопросы

1. Структура окна редактора Matlab.

2. Правила работы с m-файлами.

3. Файлы-сценарии и файлы-функции

4. Правила просмотра результатов операций.

5. Правила создания двумерных графиков.

6. Запуск и отладка программ.

Лабораторная работа № 3

Многомерные вычисления и визуализация результатов в среде Matlab

Цель работы.

1. По указанной литературе изучить:

- Правила использования операторов управления,

- правила организация вложенных циклов,

- правила получения многомерных результатов,

- вывод многомерных данных в табличной форме,

- объемная графика,

- контурная графика.

2. Разработать алгоритмы решения задач из варианта задания.

3. Составить программы решения задач.

Теоретическая часть

Существуют четыре основных оператора управления последовательностью исполнения инструкций:

· оператор условия if, в сочетании с оператором else и elseif выполняет группу инструкций в соответствии с некоторыми логическими условиями;

· оператор переключения switch, в сочетании с операторами case и otherwise выполняет различные группы инструкций в зависимости от значения некоторого логического условия;

· оператор условия while выполняет группу инструкций неопределенное число раз, в соответствии с некоторым логическим условием завершения;

· оператор цикла for выполняет группу инструкций фиксированное число раз. Все операторы управления включают оператор end, чтобы указать конец блока, в котором действует этот оператор управления.

1. Оператор условия

Оператор условия if .... end вычисляет некоторое логическое выражение и выполняет соответствующую группу инструкций в зависимости от значения этого выражения. Если логическое выражение истинно, то MATLAB выполнит все инструкции между if и end, а затем продолжит выполнение программы в строке после end. Если условие ложно, то MATLAB пропускает все утверждения между if и end и продолжит выполнение в строке после end.

Операторы if ... else ... end и if ... elseif ... end создают дополнительные ветвления внутри тела оператора if:

Оператор else не содержит логического условия. Инструкции, связанные с ним, выполняются, если предшествующий оператор if (и возможно elseif ) ложны. Оператор elseif содержит логическое условие, которое вычисляется, если предшествующий оператор if (и возможно elseif) ложны. Инструкции, связанные с оператором elseif выполняются, если соответствующее логическое условие истинно.

Оператор elseif может многократно использоваться внутри оператора условия if.

2. Оператор переключения

Синтаксис:

         switch <выражение>
                    % выражение - это обязательно скаляр или строка
         case <значение1>
                        инструкции
                    % выполняются, если < выражение> =< значение1>
         case <значение2>
                        инструкции
                    % выполняются, если <выражение> = < значение2>
         ...
         otherwise
                        инструкции
                    % выполняются, если <выражение> не совпало ни с одним из
                    %значений
         end

Оператор switch ... case 1 ... case k ... otherwise ... end выполняет ветвления, в зависмости от значений некоторой переменной или выражения.

Оператор переключения включает:

- Заголовок switch, за которым следует вычисляемое выражение (скаляр или строка).

- Произвольное количество групп case; Заголовок группы состоят из слова case, за которым следует возможное значение выражения, расположенное на одной строке. Последующие строки содержат инструкции, которые выполняются для данного значения выражения. Выполнение продолжается до тех пор, пока не встретится следующий оператор case или оператор otherwise. На этом выполнение блока switch завершается

- Группа otherwise. Заголовок включает только слово otherwise, начиная со следующей строки размещаются инструкции, которые выполняются, если значение выражения оказалось не обработанным ни одной из групп case. Выполнение завершается оператором end.

- Оператор end является последним в блоке переключателя.

Оператор switch работает, сравнивая значение вычисленного выражения со значениями групп case. Для числовых выражений оператор case выполняется, если <значение>== <выражение>. Для строковых выражений, оператор case истинен, если strcmp(значение, выражение) истинно.

3. Оператор цикла с неопределенным числом операций

Синтаксис:

          while выражение
             инструкции
          end

Описание:

Оператор цикла с неопределенным числом операций while ... end многократно выполняет инструкцию или группу инструкций, пока управляющее выражение истинно.

Если выражение использует массив, то все его элементы должны быть истинны для продолжения выполнения. Чтобы привести матрицу к скалярному значению, следует использовать функции any и all.

Задание к работе

Задача 1 Двумерная функция и объемные графики в своих окнах.

- Ввести исходные данные.

- Вычислить двумерную функцию.

- Вывести функцию в виде 5 трехмерных графиков разного типа.

- Вывести функцию в виде 2 контурных графиков разного типа.

Задача 2 Двумерная функция и объемные графики в подокнах общего окна.

Варианты заданий

№	Функция	Пределы изменения
№	Функция	Х	у
1	z = sin(x)cos(y)	от -2π до 2π	от -2π до 2π
2	z = sin(x/2)cos(y)	от -2π до 2π	от -2π до 2π
3	z = sin(2x)cos(y)	от -2π до 2π	от -2π до 2π
4	z = sin(x)cos(y/2)	от -2π до 2π	от -2π до 2π
5	z = sin(x/2)cos(2y)	от -2π до 2π	от -2π до 2π
6	z = sin(2x)cos(2y)	от -2π до 2π	от -2π до 2π
7	z = (1+sin(x)/x) (sin(y)/y)	от -2π до 2π	от -2π до 2π
8	z = (sin(x)/x)cos(y)	от -2π до 2π	от -2π до 2π
9	z = (sin(x)/x)\|cos(y)\|	от -2π до 2π	от -2π до 2π
10	z = (sin(x)/x)y	от -2π до 2π	от -2π до 2π
11	z = (sin(x)/x)\|y\|	от -2π до 2π	от -2π до 2π
12	z = (sin(x)/x) sin(y)	от -2π до 2π	от -2π до 2π
13	z = (sin(x)/x) \|sin(y)\|	от -2π до 2π	от -2π до 2π
14	z = (sin(x)/x) (1-y)	от -2π до 2π	от -2π до 2π
15	z = (sin(x)/x)\|y+0.5\|	от -2π до 2π	от -2π до 2π

Методические указания

1. В работе предусмотрены 2 задачи, в каждой из которых вычисляется двумерная функция, описывающая объемную фигуру, и строятся поверхностные и контурные графики с использованием различных графических функций. В первое задаче каждый график выводится в свое окно, во второй в подокна общего окна.

2. Для формирования поверхностного или контурного графика необходимо:

- задать число точек по координатам X и Y,

- создать вложенные циклы по X и Y, и вычислить функцию Z=f(X,Y),

- ввести номер графического окна, вывести туда график выбранного типа.

3. Следует использовать графики:

- трехмерный с аксонометрией, функция plot3(X,Y,Z),

- трехмерный с функциональной окраской, функция mesh(X,Y,Z),

- трехмерный с функциональной окраской и проекцией, функция meshc(X,Y,Z),

- трехмерный с функциональной окраской и проекцией, функция surf(X,Y,Z)

- контурный, функция contour(X,Y,Z),

- объемный контурный, функция contour3(X,Y,Z),

- трехмерный с освещением, функция surfl(X,Y,Z).

4. В каждом окне можно рисовать несколько графиков с наложением друг на друга. В списке параметров для каждого графика параметры перечисляются группами последовательно (в работе график для окна один). В каждую группу входят:

- X – первая координата площадки основания,

- Y – вторая координата площадки основания,

- Z – значение функции.

Пример выполнения

Задание

Функция 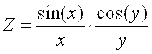Пределы изменения аргументов -2π….2π

Задача 1

% Задача 1

% Число точек и шаг

N=40;

h=pi/20;

% Расчет матрицы

for n=1:2*N+1

if n==N+1 A(n)=1; else A(n)=sin(h*(n-N-1))/(h*(n-N-1)); end;

end;

for n=1:2*N+1

for m=1:2*N+1

Z(n,m)=A(n)*A(m);

end;

% Задание площадки

[X,Y]=meshgrid([-N:1:N]);

% Вывод графика в аксонометрии в окно 1

figure(1);

plot3(X,Y,Z);

% Вывод трехмерного графика с функциональной окраской в окно 2

figure(2);

mesh(X,Y,Z);

% Вывод трехмерного графика с функциональной окраской и проекцией в окно 3

figure(3);

meshc(X,Y,Z);

% Вывод трехмерного графика с проекцией в окно 4

figure(4);

surf(X,Y,Z);

% Вывод контурного графика в окно 5

figure(5);

contour(X,Y,Z);

% Вывод объемного контурного графика в окно 6

figure(6);

contour3(X,Y,Z);

% Вывод объемного графика с освещением в окно 7

figure(7);

surfl(X,Y,Z);

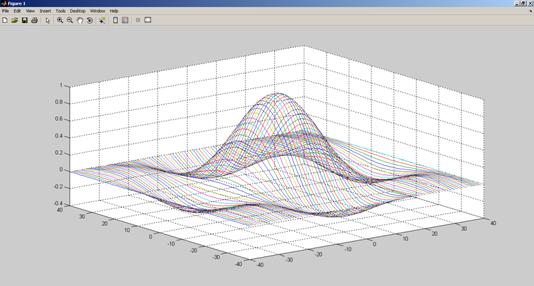
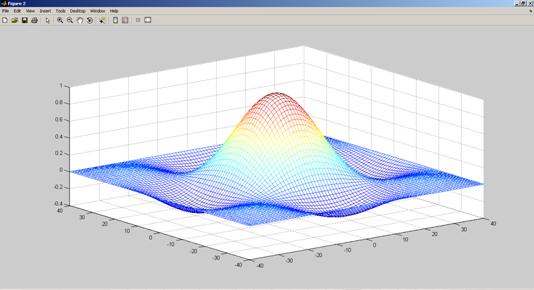
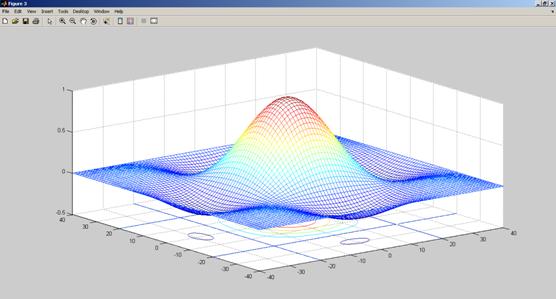
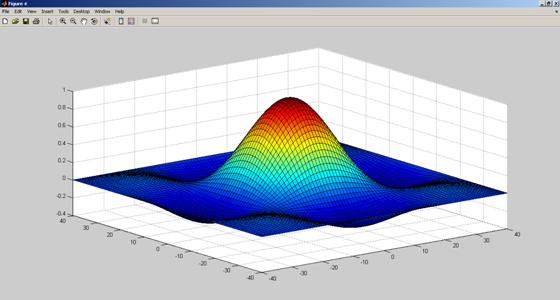
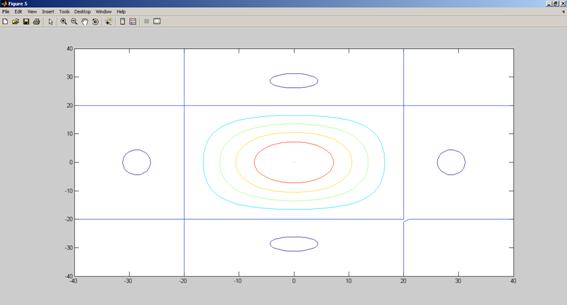
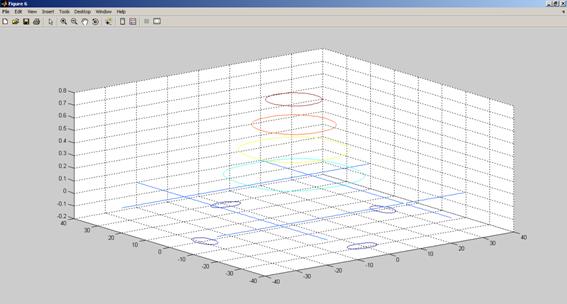
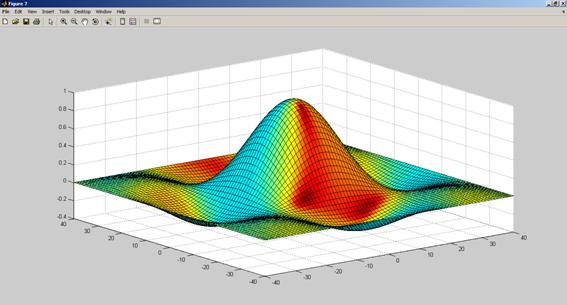
Рис. 3.1. Результат выполнения программы (задача 1)-графики выводятся в отдельных окнах

Задача 2

% Задача 2

% Число точек и шаг

N=40;

h=pi/20;

% Расчет матрицы

for n=1:2*N+1

if n==N+1 A(n)=1; else A(n)=sin(h*(n-N-1))/(h*(n-N-1)); end;

end;

for n=1:2*N+1

for m=1:2*N+1

Z(n,m)=A(n)*A(m);

end;

% Задание площадки

[X,Y]=meshgrid([-N:1:N]);

% Вывод графика в аксонометрии в подокно 1

subplot(3,3,1),plot3(X,Y,Z);

% Вывод трехмерного графика с функциональной окраской в подокно 2

subplot(3,3,2),mesh(X,Y,Z);

% Вывод трехмерного графика с функциональной окраской и проекцией в подокно 3

subplot(3,3,3),meshc(X,Y,Z);

% Вывод трехмерного графика с проекцией в подокно 4

subplot(3,3,4),surf(X,Y,Z);

% Вывод контурного графика в подокно 5

subplot(3,3,5),contour(X,Y,Z);

% Вывод объемного контурного графика в подокно 6

subplot(3,3,6),contour3(X,Y,Z);

% Вывод объемного графика с освещением в подокно 7

subplot(3,3,7),surfl(X,Y,Z);

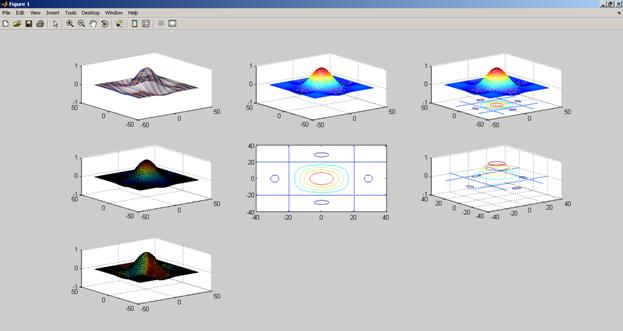
Рис. 3.2. Результат выполнения программы (задача 2)-графики выводятся в одном окне

Контрольные вопросы

1. Организация вложенных циклов.

2. Правила задания многомерных функций.

3. Связь двумерной функции с матрицей для вывода графиков.

4. Вывод многомерных результатов в форме таблицы.

5. Трехмерная графика в аксонометрии.

6. Трехмерная графика с функциональной раскраской

7. Трехмерная графика с функциональной раскраской и проекцией.

8. Контурная графика.

9. Объемная контурная графика.

10. Объемная графика с освещением.

Лабораторная работа №4

Моделирование устройства с помощью Simulink.

Цель работы:

1. По указанной литературе изучить:

· основы Simulink,

· правила создания моделей в Simulink,

· иерархическую библиотеку Simulink.

2. Разработать структура модели устройства для варианта задания.

Теоретическия часть.

1. Назначение Simulink

Пакет Simulink является приложением к MATLAB. При моделировании с использованием Simulink реализуется принцип визуального программирования, в соответствии с которым, пользователь на экране из библиотеки стандартных блоков создает модель устройства и осуществляет расчеты. При этом, в отличие от классических способов моделирования, пользователю не нужно досконально изучать язык программирования и численные методы математики, а достаточно общих знаний, требующихся при работе на компьютере и, естественно, знаний той предметной области, в которой он работает.

Для построения функциональной блок-схемы моделируемых устройств Simulink имеет обширную библиотеку блочных компонентов и удобный редактор блок-схем. Он основан на графическом интерфейсе пользователя и по существу является типичным средством визуально-ориентированного программирования. Используя палитры компонентов (наборы), пользователь с помощью мыши переносит нужные блоки с палитр на рабочий стол пакета Simulink и соединяет линиями входы и выходы блоков. Таким образом, создается блок-схема системы или устройства, то есть модель.

2. Моделирование в Simulink

2.1. Запуск и построение модели.

Для запуска программы необходимо:

1. Первое действие – запустить Matlab. При этом возникает стартовое диалоговое окно, в котором три встроенных окна: Command Window (командное) – справа, Launch Pad (Средства запуска) – в левом верхнем углу, Command History (История команд) – в левом нижнем углу. Каждое подокно можно освободить из дока.

2. Для создания модели нужно выполнить действие File→New→Model. Это приводить к запуску программы Simulink, которая создает пустое окно модели.

Рис 4.1. Пустое окно модели

3. Далее нужно вызвать браузер библиотеки компонент, используя меню или кнопку в панели инструментов Library Brouser. Окна браузера содержит две панели: слева иерархическое дерево библиотеки, справа – содержимое выбранной в левой панели папки с блоками.

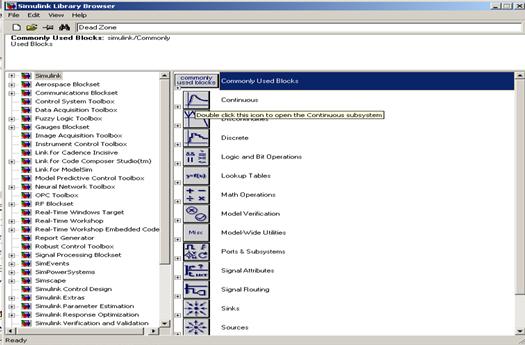
Рис 4.2. Библиотека компонент

В папке могут быть подбиблиотеки и блоки. Каждый блок и подбиблиотека имеет визуальный семантический образ и надпись.

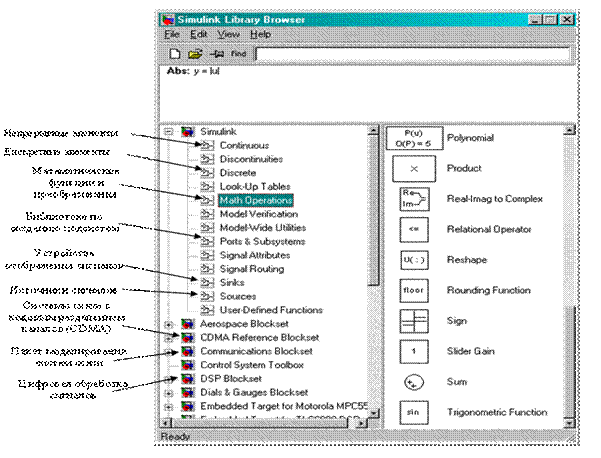
Рис.4.3. Основные библиотеки Simulink.

4. Расположить блоки в окне модели. Для этого необходимо открыть соответствующий раздел библиотеки (Например, Sources - Источники). Далее, указав курсором на требуемый блок и нажав на левую клавишу мыши – «перетащить» блок в созданное окно. Затем необходимо соединить блоки коннекторами. Для этого нужно протаскивать мышь от одной соединяемой точки к другой. При отпускании кнопки мыши в модели отображается коннектор со стрелкой.

На рис. 5.4 показано окно модели, содержащее блоки.

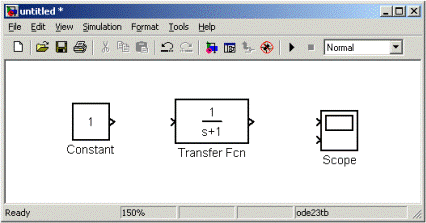
Рис 4.4. Окно модели, содержащее блоки

5. Установить для каждого блока свойства. Для этого нужно на блоке сделать двойной щелчок мышью, что приведет к появлению окна со свойствами блока. Установите нужные свойства в полях окна

2.2. Основные блоки для моделирования динамических систем

Обозначение

Назначение блока

Раздел библиотеки

Constant

Step

Ramp

Sine Wave

Random Number

From Workspace

From File

Signal Builder

Saturation

Integrator

Derivative

Sum

Product

Gain

Math Function

Trigonometric

Relational Operator

Logical Operator

Fcn

MATLAB Fcn

Scope

XY Graph

Display

To Workspace

To File

Stop

Goto

From

Mux

Постоянное воздействие

Одиночный перепад (толчок)

Наклонная линия k*t

Синусоидальное воздействие a*sin (wt)

Случайный сигнал

Сигнал из рабочей области

Сигнал из файла

Конструктор сигналов

Блок ограничения

Интегрирующий блок

Дифференцирующий блок

Суммирующий блок (+ и -)

Блок умножения и деления (* и /)

Блок масштабирования

Блок математических функций

Блок тригонометрических функций

Операции отношения

Логические операции

Блок задания функции

Блок задания m-функции

Виртуальный осциллограф

Виртуальный графопостроитель

Регистратор значений

Запись в рабочую область

Запись в файл

Блок остановки работы

Передача данных без соединения

Получение данных без соединения

Мультиплексор данных

Sources

Nonlinear

Continuous

Math

Continuous

Math

Functions & Tables

Sinks

Signal & Systems

2.3. Состав основной библиотеки блоков

В Simulink содержатся следующие библиотеки:

• Continuous – компоненты c непрерывными характеристиками;

• Discontinious – компоненты c разрывными характеристиками;

• Discrete – дискретные компоненты;

• LookUp Table – табличное задание зависимостей;

• Math Operations – математические компоненты;

• Model Verifications – верификация моделей;

• Model_Wide Utilities – дополнительные утилиты;

• Port & Subsystem – порты и подсистемы;

• Signal Attributes – блоки атрибутов сигналов;

• Signal Routing – блоки маршрутизации сигналов;

• Functions & Tables – функции и таблицы;

• Nonlinear – нелинейные компоненты;

• Connections – соединительные компоненты;

• Signals & Systems – сигналы и системы;

• Sinks – регистрирующие устройства;

• Sources – источники сигналов и воздействий;

• User_Defined Functions – функции, задаваемые пользователем.

3. Команды управления моделированием

Команда

Назначение команды

Sim

Sldebug

Simset

Simget

Linmod

Dlinmod

Trim

close_system

new_system

open_system

load_system

save_system

add_block

add_line

delete_block

delete_line

find_system

hilite_system

replace_block

set_param

get_param

Bdclose

Bdroot

Gcb

Gcbh

Gcs

Getfullname

Запустить модель Simulink

Отладить модель Simulink

Определить параметры структуры SIM

Выдать параметры структуры SIM

Выделить линейную модель из системы

Выделить линейную модель из дискретной системы

Найти рабочую точку устойчивого состояния

Закрыть модель или блок.

Создать новое окно с пустой моделью

Открыть существующую модель или блок

Загрузить существующую модель без визуализации

Сохранить открытую модель

Добавить новый блок

Добавить новую строку

Удалить блок

Удалить строку

Найти модель

Засветить объекты без модели

Заменить существующие блоки новыми блоками

Установить значения параметров для модели или блока

Выдать значения параметров моделирования модели

Закрыть окно Simulink

Установить корневой уровень для имени модели

Выдать имя текущего блока

Выдать дескриптор текущего блока

Выдать имя текущей системы

Выдать полный путь для блока

Задание к работе

Задача 1. Простая модель устройства в соответствии с вариантом задания.

· Создать модель. В ней сигнал от источника поступает на функциональный блок. Регистратор с двумя входами позволяет наблюдать сигналы на входе и выходе функционального блока.

· Провести ее моделирование.

Задача 2. Расширенная модель устройства в соответствии с вариантом задания.

· Создать модель. В ней к модели задачи 1 добавляется параллельная ветвь с вторым функциональным блоком. Регистратор с тремя входами позволяет наблюдать сигналы на входах и выходах функциональных блоков.

· Провести ее моделирование.

Варианты заданий

№

Источник сигнала

Блоки

Первый

Дополнительный

Sine Wave

Синус

Gain

Усиление

Derivate

Дифференциатор

Pulse Generator

Импульсы

Saturation

Ограничитель

Integrator

Интегратор

Repeating Sequence

Пила

Quantizer

Квантизатор

Gain

Усиление

Ram

Линейно нарастающий

Derivate

Дифференциатор

Saturation

Ограничитель

Chirp Signal

Переменной частоты

Integrator

Интегратор

Quantizer

Квантизатор

Sine Wave

Синус

Transport delay

Задержка

Derivate

Дифференциатор

Pulse Generator

Импульсы

Dead Zone

Мертвая зона

Integrator

Интегратор

Repeating Sequence

Пила

Gain

Усиление

Transport delay

Задержка

Ram

Линейно нарастающий

Saturation

Ограничитель

Dead Zone

Мертвая зона

Chirp Signal

Переменной частоты

Quantizer

Квантизатор

Gain

Усиление

Sine Wave

Синус

Derivate

Дифференциатор

Saturation

Ограничитель

Pulse Generator

Импульсы

Integrator

Интегратор

Quantizer

Квантизатор

Repeating Sequence

Пила

Transport delay

Задержка

Derivate

Дифференциатор

Ram

Линейно нарастающий

Dead Zone

Мертвая зона

Transport delay

Задержка

Chirp Signal

Переменной частоты

Derivate

Дифференциатор

Saturation

Ограничитель

В таблице названия функциональных блоков даны на русском и английском языках (так, как они названы в браузере библиотеки блоков Simulink).

Методические указания

1. Модель устройства содержит источник сигнала, функциональные блоки и средства наблюдения за поведением системы (дисплей, численный индикатор и др.).

2. Во всех вариантах задания нужно использовать дисплей с одним входом в задаче 1 и с двумя входами в задаче 2.

Пример выполнения

Задание

Задача 1. Двусторонний ограничитель синусоидального сигнала.

· Создать модель.

· Провести ее моделирование.

Задача 2. Двусторонний ограничитель синусоидального сигнала и блок мертвой зоны.

· Создать модель.

· Провести ее моделирование.

Задача 1

1. Создать на экране дисплея пустое окно модели и вызвать браузер библиотеки блоков.

2. Открыть в браузер папку с блоками источников, используя кнопку подбиблиотеки Sources (Источники). Из подбиблиотеки Sources левой кнопкой мыши перетащить в окно модели блок Sine Wave (генератор синусоида) и там отпустить в удобном месте.

3. Двойным щелчком по блоку Sine Wave в модели вызвать окно со свойствами блока. В его полях выбрать параметры. В данном случае установить амплитуду и частоту (фазу и время отсчета можно не менять).

4. Открыть в браузере окно нелинейных блоков, используя кнопку подбиблиотеки Nonlinear (Нелинейные). Из подбиблиотеки Nonlinear левой кнопкой мыши перетащить в окно модели блок Saturation (ограничитель) и там отпустить удобном месте.

5. Двойным щелчком по блоку Saturation в модели вызвать окно со свойствами блока. В нем установить верхний и нижний пределы ограничения.

6. Открыть браузере окно блоков регистраторов, используя кнопку подбиблиотеки Sinks (Регистраторы). Из подбиблиотеки Sinks левой кнопкой мыши перетащить в окно модели блок Scope и там отпустить удобном месте.

7. Двойным щелчком по блоку Scope в модели вызвать его в демонстрационное окно. Разместить это окно на экране в удобном месте, перемещая его за заголовок левой кнопкой мыши.

8. Кнопкой Properties (Свойства) окна Scope вызвать окно свойств, в котором установить число осей 2 (для входного и выходного ограничителя).

9. Левой (или правой) кнопкой мыши соединить блоки. При нажатой левой кнопке курсор имеет форму крестика, который надо позиционировать по помеченным входам и выходам блоков. Начать надо с помеченного выхода одного блока и отпустить кнопку на помеченном входе другого. Первый вход регистратора соединить со входом ограничителя, второй - с выходом.

10. Результат – модель устройства и пустое окно регистратора.

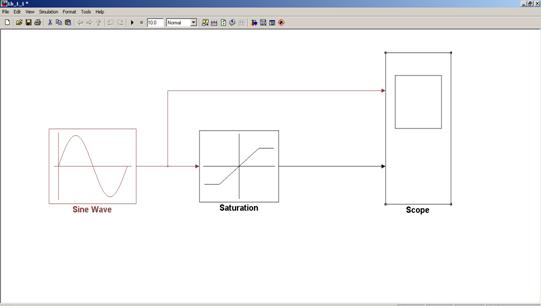
Рис 4.5. Модель устройства

11. Включить симулирование (моделирование) командной Simulation→Start (или кнопкой на панели инструментов модели). В окне Scope отображаются графики сигналов.

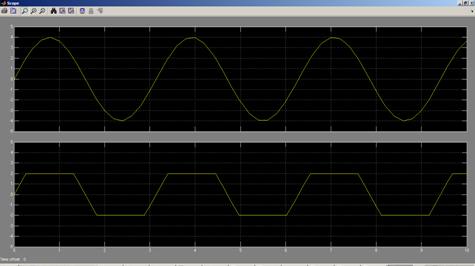
Рис 4.6. График сигнала на экране осциллографа

Если результат не совпадает с ожидаемым, то нужно изменить параметры модели. Команды Simulation → Simulation parameters вызывает окно параметров модели, в котором можно сделать изменения. Можно регулировать параметры, размещенные на 5 вкладах:

· Solver – решатель (время начало и конца, пошаговой или непрерывный режим, используемый математический метод, шаг моделирования, погрешности вычислений и др.).

· Workspace I/O – рабочая область (параметры загрузка и сохранения, опции сохранения).

· Diagnostics – диагностика (параметры и области, опции конфигурации, действия).

· Advanced – Расширения (признаки оптимизации).

· Real-Time Workshop – работа в реальном времени (выбор конфигурации целевого объекта и параметров для нее).

12. Если график получился в неудобном масштабе, то масштаб можно изменить, для этого лучше выбрать режим Autoscale (автомасштабирование) в локальном меню, вызываемым щелчком правой кнопки мыши по графику. Ниже видны результате автомасштабирования.

Задача 2

1. Добавим в модель в параллельную ветвь блок Dead Zone (Мертвая зона). Установим его параметры.

2. У регистратора Scope изменим число осей на 3.

3. Соединим третий вход Scope с выходом Dead Zone. Соединим вход Dead Zone с выходом Sine Wave.

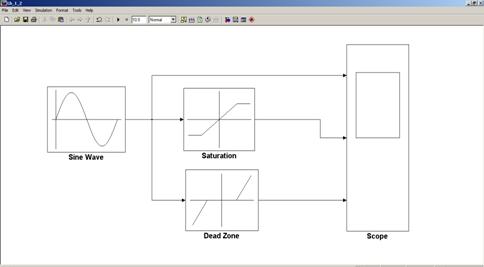
Рис 4.7. Модель устройства с использованием блока Dead Zone

4. Выполнить моделирование. В окне Scope графики выходных сигналов.

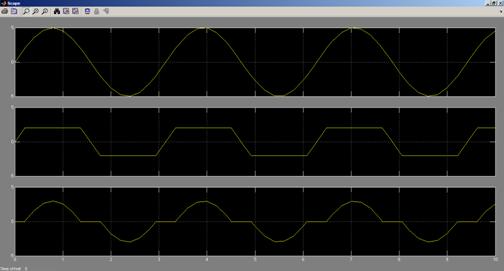
Рис 4.8. График выходного сигнала на экране осциллографа

Контрольные вопросы

1. Назначение Simulink.

2. Правила построения моделей в Simulink.

3. Структура иерархической библиотеки Simulink.

4. Блоки из папки Continuous библиотеки Simulink.

5. Блоки из папки Discrete библиотеки Simulink.

6. Блоки из папки Functions & Tables библиотеки Simulink.

7. Блоки из папки Math библиотеки Simulink.

8. Блоки из папки Nonlinear библиотеки Simulink.

9. Блоки из папки Signal & Systems библиотеки Simulink.

10. Блоки из папки Sources библиотеки Simulink.

11. Блоки из папки Sinks библиотеки Simulink.

12. Блоки из Communication Blockset

13. Другие наборы блоков.

14. Команды управления моделированием.

Лабораторная работа №5

Моделирование аналогового сигнала в Matlab и Simulink

Цель работы:

Теоретическая часть.

1. Дискретизация сигналов

Обычно все сигналы являются аналоговыми. Чтобы использовать аналоговый сигнал в цифровых системах необходимо преобразовать аналоговый сигнал в цифровой. Этот процесс состоит из дискретизации и квантования.

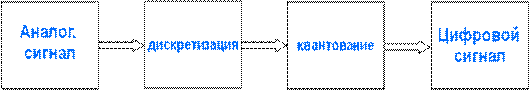
Рис. 5.1. Преобразование аналогового сигнала в цифровой

Процесс преобразования аналогового сигнала в дискретный называется дискретизацией.

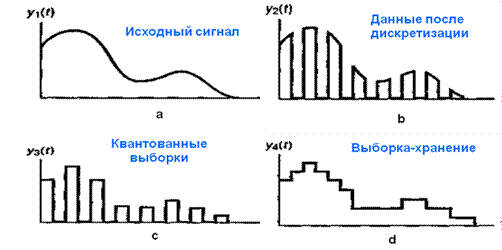
Рис. 5.2. Дискретизация сигнала

2. Моделирование дискретных сигналов в Matlab

Генерировать сигналы в Matlab можно тремя способами:

· в диалоговом режиме, с помощью последовательности команд в командном окне;

· в автоматическом режиме, путем создания и запуска на выполнение m-скрипта;

· в автоматическом режиме, путем создания и вызова m-функции.

Генерирование сигналов в диалоговом режиме. Этот способ наиболее трудоемок, поскольку требует каждую команду набирать с клавиатуры в командном окне. Чтобы повысить производительность труда, можно всю последовательность команд предварительно набрать в любом текстовом редакторе (обычно это Notebook или Word), а затем, скопировав текст в буферную память (Clipboard), вставить его в командное окно. Недостаток этого способа в том, что необходимо одновременно держать активными две программы – Matlab и текстовый редактор. Достоинство данного способа проявляется тогда, когда работу в Matlab производят, следуя некоей инструкции, в которой теоретические сведения чередуются с практическими заданиями в виде фрагментов текстов m-скриптов.

Генерирование сигналов путем создания m-скрипта. Данный способ отличается тем, что все команды набираются в специальном окне редактора m-файлов (рис.5.3).

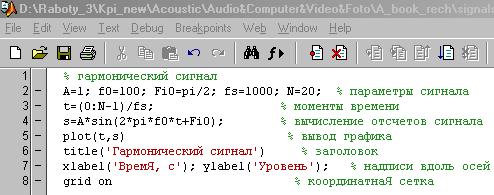
Рис. 5.3. Окно редактора m-файлов

Данный способ хорош тем, что вместо сторонних программных продуктов используется собственный инструментарий Matlab, специализированный для написания и отладки m-скриптов.

Генерирование сигналов путем создания m-функции. Данный способ отличается тем, что входные данные записываюткак аргумент некоей функции , а выходные – как значение этой функции. Удобство в том, что символьные обозначения данных могут отличаться от обозначений, используемых в теле функции. Более того, числовые значения входных данных можно просто задавать в наименовании вызываемой функции.

3. Моделирование обработки сигналов в Simulink

Simulink обеспечивает чрезвычайно обширные возможности создания программ обработки сигналов для современных научных и технических приложений.

Подключающаяся к Simulink мощная подсистема имитационного моделирования в реальном масштабе времени (при наличии дополнительных аппаратных средств в виде плат расширения компьютера), представленная пакетами расширения Real Time Windows Target и Workshop, — мощное средство управления реальными объектами и системами. Достоинством такого моделирования является его математическая и физическая наглядность. В компонентах моделей Simulink можно задавать не только фиксированные параметры, но и математические соотношения, описывающие поведение моделей.

Пакет может применяться, в частности, в таких областях, как обработка аудио- и видеоинформации, телекоммуникации, геофизика, задачи управления в реальном режиме времени, экономика, финансы и медицина.

Задание к работе:

Задача 1. Сгенерировать сигнал на выходе модели (с частотой дискретизации ), если на вход подается сигнал:

Генерацию сигнала реализовать в среде Matlab путем создания m-функции

Задача 2. Сгенерировать этот же сигнал , но генерацию сигнала реализовать в среде Simulink.

Сравнить результаты моделирования в средах Matlab и Simulink.

Варианты:

Параметры сигнала

Вариант Параметр	1	2	3	4	5	6	7	8
	1	1	2	1	1	1	1	2
	1	2	1	1	1	2	2	1
, Hz	100	100	100	100	100	100	100	100
, Hz	200	200	200	200	200	200	200	200
, rad	0	0	0	0		0		0
, rad	0	0	0		0		0

Частота дискретизации = 1/Dt ³ 2f_max

Методические указания:

1. Сигнал может генерироваться двух типов: непрерывный и дискретный. Для моделирования работы непрерывных систем рекомендуют использовать непрерывный тип time-based, а для моделирования работы дискретных систем – дискретный тип sample-based

2. Если установлен тип time-based, тогда параметр Sample time может принимать значения:

· 0 (по умолчанию) – блок работает в непрерывном режиме;

· >0 - блок работает в дискретном режиме;

· -1 – блок наследует тот же режим, что и принимающий блок.

3. Дискретизацию сигнала в непрерывном режиме можно реализовать с помощью блока Zero-Order Hold.

Блок Zero-Order Hold можно трактовать как “дискретизатор”, т.е. часть АЦП, ответственную за дискретизацию сигнала. Иногда блок Zero-Order Hold именуют АЦП. В блоке Zero-Order Hold, однако, квантование не производится.

4. Работа в дискретном режиме (sample-based) заставляет блок вести себя так, как если бы к выходу непрерывного генератора был присоединен блок Zero-Order Hold. Собрав две схемы (рис.5.4) и задав в обоих случаях значение параметра Sample time, равное 0.5 (рис.5.5), получаем идентичные результаты (рис.5.6).

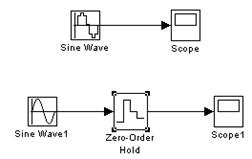
Рис. 5.4. Схемы, собранные в непрерывном и дискретном режимах

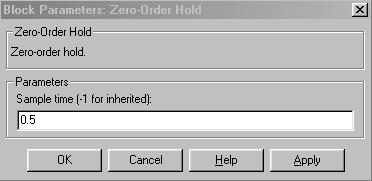
Рис. 5.5. окно настройки блока Zero-Order Hold

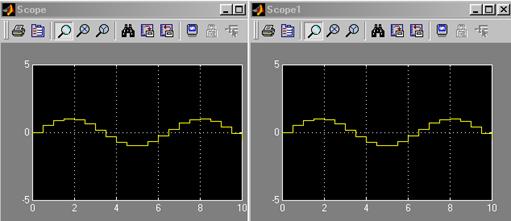
Рис. 5.6. Графики на экранах осциллографов в непрерывном и дискретном режимах

Сигнал работе блока генерации в режиме непрерывного времени имеет вид гладкой функции времени, а в режиме дискретного времени - вид ступенчатого сигнала, такого, как если бы к выходу генератора плавного сигнала был подсоединен блок Zero-Order Hold, являющийся дискретизатором типа “отсчет-хранение”.

Иными словами, задавая режим дискретного времени, мы уходим от необходимости в использовании блока Zero-Order Hold.

5. Построение графиков.

Помимо блока Scope, график можно построить и с помощью блока X-Y-Graf, на верхний вход X которого нужно подать последовательность моментов времени с помощью блока Clock (часы), а на нижний вход Y – значения генерируемого сигнала (рис.5.7).

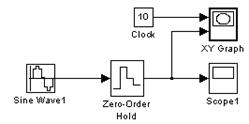
Рис.5.7. Использование блока X-Y-Graf для построения сигнала

В результате предварительно настроенный (в соответствующем окне настройки задаются граничные значения аргумента и функции, а также указывается значение параметра Sample time) графопостроитель выдаст показанный график (рис.5.8, a), если для блока X-Y-Graf задано Sample time=-1 (т.е. период дискретизации наследуется).

График будет несколько иным (рис.5.8, b), если для блока X-Y-Graf задано Sample time=0.5.

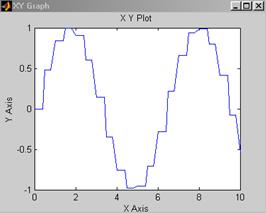
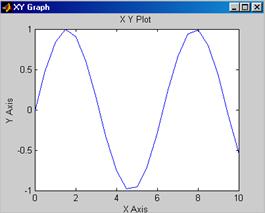
a) b)

Рис. 5.8. Результат построения графика сигнала при различных парметрах Sample time

6. Массивы отсчетов моментов времени и соответствующих значений сигнала можно с помощью блока To Workspace экспортировать из среды Simulink в среду Matlab (рис.5.9).

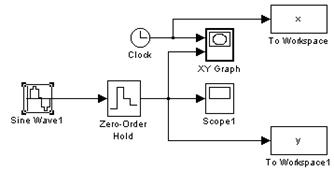
Рис.5.9. Экспорт массивов отсчетов с использованием блока To Workspace

При этом лучше всего задать формат array для экспортируемых данных (рис.5.10).

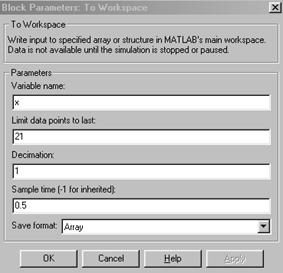
Рис.5.10. Параметры блока To Workspace

Пример выполнения:

Задача 1.

Сгенерировать N отсчетов аналогового сигнала амплитудой A, частотой f0, начальной фазой Fi0, с частотой дискретизации fs:

A=1; f0=100; Fi0=pi/2; fs=1000; N=20;

s=A*sin(2*pi*f0*t+Fi0);

Программа в среде Matlab выглядит следующим образом:

% Дискретизация сигнала

A=1; f0=100; Fi0=pi/2; fs=1000; N=20; % параметры сигнала

t=(0:N-1)/fs; % время

s=A*sin(2*pi*f0*t+Fi0); % вычисление (генерация) сигнала

plot(t,s) % график сигнала

title('Harmonic signal')

xlabel('Time, sec'); ylabel('Amplitude');

grid on

Результат выполнения:

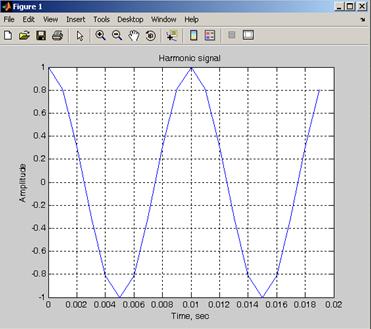
Рис. 5.11. График сгенерированного сигнала в среде Matlab

Задача 2.

Возьмем из библиотеки блоков Simulink два блока: Sine Wave и Scope:

ViewàLibrary Browser

SourcesàSine Wave

SinksàScope

Соединим их.

Рис. 5.12. Схема соединения блоков Sine Wave и Scope

Затем двойным щелчком по блоку осциллографа активизируем окно, имитирующее экран осциллографа, и запустим модель (кнопка Start simulation). В результате получим изображение отрезка синусоиды:

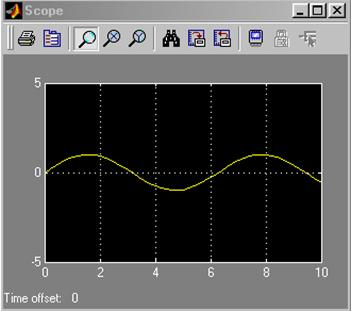
Рис. 5.13. Сигнал, полученные на выходе блока Scope

Теперь сгенерируем в Simulink отрезок дискретного гармонического сигнала с темы же параметрами, что были заданы в Matlab: амплитуда 1, частота 100 Гц, частота дискретизации 1000 Гц, начальная фаза , количество отсчетов 20.

Собираем схему из генератора и осциллографа. В окне-маске настройки генератора производим указание нужных числовых значений параметров, задаем тип time-based и присваиваем значение Sample time = 0.001 (рис.5.14).

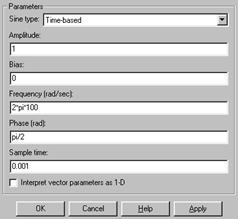
Рис. 5.14. Настройка параметров симуляции

Настраиваем параметры моделирования: задать начало и конец модельного времени (в нашем случае это 0 и 0.02 с, соответственно), а также выбрать алгоритм моделирования (тип «решателя»). На рис.5.15 показано окно настроек параметров моделирования, активизирующееся при выборе позиции меню Simulation/Simulation parameters.

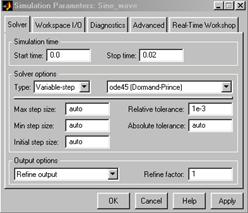
Рис. 5.15. Настройка параметров симуляции

Кроме того, настроим параметры осциллографа, щелкнув по кнопке Parameters на окне Scope (рис.5.16, a,b).

b) b)

Рис. 5.16. Настройка параметров осциллографа

После запуска модели на экране осциллографа появится изображение:

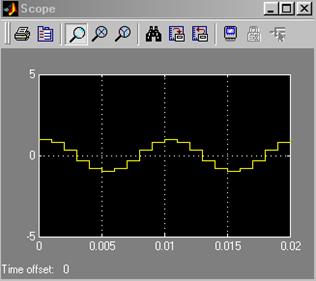
Рис. 5.17. График на экране осциллографа

Поскольку параметры осциллографа были заданы так, чтобы в рабочее пространство выводился двумерный массив ScopeData значений аргумента и функции, с помощью команд:

>> y1=ScopeData(:,1);

>> y2=ScopeData(:,2);

>> plot(y1,y2)

можно построить график сгенерированной функции средствами Matlab (рис.5.18).

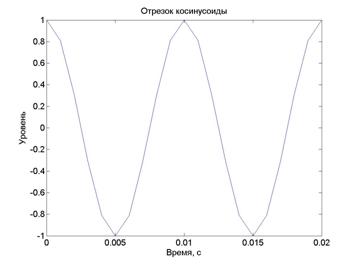
Рис. 5.18. График функции, выведенный средой Matlab

Сравнивая рис.5.11 и рис.5.18, замечаем лишь одно отличие – при моделировании в Simulink сгенерирована 21 точка, тогда как в Matlab генерировалось 20 точек. Причина различия проста: на интервале модельного времени при частоте дискретизации находится моментов времени, для которых будет сгенерирован сигнал. Очевидно, это обстоятельство легко учесть, добившись полного совпадения результатов моделирования в средах Matlab и Simulink.

Контрольные вопросы:

1. Опишите процесс преобразования сигнала из аналоговой формы в цифровую.

2. Что такое квантование сигнала?

3. Что такое дискретизация сигнала?

4. Опишите способы моделирования сигналов в Mathlab.

5. Генерирование сигналов в диалоговом режиме.

6. Генерирование сигналов путем создания m-скрипта.

7. Генерирование сигналов путем создания m-функции.

8. Опишите использование типов сигналов в Simulink (режимы time-based и sample-based).

9. Опишите реализацию дискретизации сигнала в непрерывном режиме с помощью блока Zero-Order Hold.

10. Опишите реализацию дискретизации сигнала в дискретном режиме.

Лабораторная работа № 6

Моделирование специализированного процессора обработки сигналов на основе кубических базисных сплайнов с использованием возможностей среды Matlab и Simulink

Цель работы. Изучение методов аппроксимации функциональных зависимостей кубическими базисными сплайнами, создание структуры специализированного процессора на основе кубических базисных сплайнов и его Simulink-модели.

Теоретическая часть

Под сплайном (от англ. spline — планка, рейка) обычно понимают кусочно-заданную функцию, совпадающую с функциями более простой природы на каждом элементе разбиения своей области определения.

Классический сплайн одной переменной строится так: область определения разбивается на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна. Например, непрерывная ломаная есть сплайн степени 1 и дефекта 1.

Сплайны имеют многочисленные применения, как в математической теории, так и в разнообразных вычислительных приложениях. В частности, сплайны двух переменных интенсивно используются для задания поверхностей в различных системах компьютерного моделирования.

Методы сплайн-аппроксимации служат универсальным инструментом моделирования функций и по сравнению с другими математическими методами при равных с ними информационных и аппаратных затратах обеспечивают большую точность вычислений.

Сплайн методы наиболее эффективны в случаях дискретного задания исходных данных. На отрезке [а, b] рассмотрим сетку D:

D: a = x₀ < x₁ < ...< x_n= b

Полиномиальный сплайн произвольной степени m дефекта d (d - целое число, 1£ d £ m) c узлами на сетке D определяется [59, 60, 140] как функция ,

1) 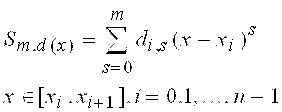(1)

Производная от сплайна порядка (m - d +1) может быть разрывной на [ a, b]. Поэтому говорят о разных порядках гладкости сплайнов: первом, втором и т.д.

В технических приложениях наиболее употребительными являются сплайны невысокой степени, в частности параболические и кубические.

Наиболее простые аналитические выражения для В - сплайнов получаются для случаев равномерного задания сеток. Приведем эти выражения для базисных элементов третьей степени.

(2)

Для сплайнов 3-й степени существует локальные формулы, локальная формула для трех точек (3-точечная формула) имеет следующий вид:

b_i = (1/6)(-f_i_-1 + 8f_i – f_i₊₁); (3)

Любой сплайн S_m (x) степени m дефекта 1, интерполирующий заданную функцию f (x) может быть единственным образом представлен В - сплайнами в виде суммы:

, (4)

где b_i – коэффициенты.

Согласно формуле (4) значение интерполируемой функции в произвольной точке заданного интервала определяется значениями лишь m+1 слагаемых – парных произведений базисных функций на постоянные коэффициенты. Например, кубические В-сплайны требуют четырех базисных слагаемых.

Значение функции вычисляется по формуле

при (5)

Остальные базисные сплайны на этом подинтервале равны нулю и, следовательно, в образовании суммы не участвуют.

Рис.6.1. Таблично-алгоритмическая вычислительная структура для реализации аппроксимации функций кубическими базисными сплайнами.

Задание к работе:

Построить Simulink – модель специализированного процессора обработки сигналов на основе кубических базисных сплайнов.

В качестве входного сигнала использовать сигнал, полученный в результате выполнения лабораторной работы №5.

Методические указания:

При построении Simulink–модели следует использовать следующие блоки:

1. Signal From Workspace - сигнал из рабочей области. Импорт сигнала из рабочего пространства MATLAB

Расположение: в библиотеке источников обработки сигналов (Library: Signal Processing Sources)

Вид:

Блок From Workspace служит для получения данных из рабочего пространства. В качестве параметров задаются формат матрицы данных (по умолчанию [T, U]) и эталонное время Sample time (по умолчанию 0).

Кроме того, имеется список для задания конечного значения путем:

• Interpolate data – экстраполяции данных;

• Setting to zero – установки на нуль;

• Hold final data value – задержки последнего значения данных, что бывает нужно для его представления регистрирующими блоками;

• Cyclic Repetition – циклического повторения.

При включении флажка Interpolate data производится интерполяция данных на промежутке времени до tfinal, а для значений времени, больших tfinal, выполняется экстраполяция по последним отсчетам данных (при снятии флажка сигнал на указанных интервалах обнуляется). В матрице источника From Workspace отсчеты времени занимают первый столбец, а не строку.

2. Product - Умножение и деление скалярных и нескалярных величин.

Расположение: в библиотеке математических операций (Library: Math Operations)

Вид:

Наряду с умножением скалярных сигналов может использоваться и для вычисления произведения векторов и матриц.

По умолчанию значения параметров:

· Умножение: поэлементно (.*)

· Количество входов: 2

В окне параметров этого блока можно задать число его входов, то есть блок можно использовать и при числе сомножителей более 2.

Блок Product предназначен не только для умножения, но и для деления. При этом операции задаются подобно тому, как это было описано для блока суммирования/вычитания с применением знаков умножения * или деления / в шаблоне.

3. Sum - Сумма, сложение, вычитание элементов

Расположение: в библиотеке математических операций (Library: Math Operations)

Вид:

Блок выполняет сложение или вычитание величин или сигналов, поданных на его входы. Этот блок может производить операции сложения или вычитания над скаляром, вектором или матрицей входов.

4. XY Graph - Блок XY отображает график в координатных плоскостях XY из его входов в окне MATLAB.

Расположение: в библиотеке приемников данных (Library: Sinks)

Вид:

Блок имеет два скалярных входа. На вход Y подается сигнал одной временной зависимости, а на вход X – другой. Фазовый портрет двух временных зависимостей (например, напряжения и тока в электрической цепи) строится в виде параметрически заданного графика.

В отличие от осциллографа, виртуальный графопостроитель имеет входы по осям X и Y, что позволяет строить графики функций в полярной системе координат, фигуры Лиссажу, фазовые портреты и т. д. Установка параметра Simple Time равным –1 позволяет получать синусоиду с достаточно большим числом точек. При этом ее график получается плавным.

5. Clock - обеспечивает время моделирования

Расположение: в библиотеке Источники (Library: Sources)

Вид:

Источник текущего времени Clock служит для генерации чисел, которые являются значениями текущего времени моделирования на каждом шаге моделирования. Этот блок используется для других блоков, которые используют время моделирования.

Для контроля этого времени может использоваться цифровой индикатор – Display. Параметром источника является шаг Decimation, с которым меняются отсчеты времени. Флажок Display time задает отображение времени в блоке источника.

6. To Workspace - Запись данных в рабочее пространство

Расположение: в библиотеке приемников данных (Library: Sinks)

Вид:

Блок записывает указанную матрицу (но без строки отсчетов времени) в рабочее пространство. В окне параметров блока To Workspace задается формат записи: структура Structure, структура со временем Structure with time и массив Array.

Пример выполнения:

Рис.6.2. Simulink – модель специализированного процессора обработки сигналов на основе кубических базисных сплайнов.

Simulink – модель спецпроцессора восстановления сигналов на основе кубических базисных сплайнов (рис.6.2) состоит из восьми запоминающего устройства данных (Signal From Workspace), четерёх умножителей (Product), одного сумматора (Sum), блок визуализации полученных сигналов (XY Graph).

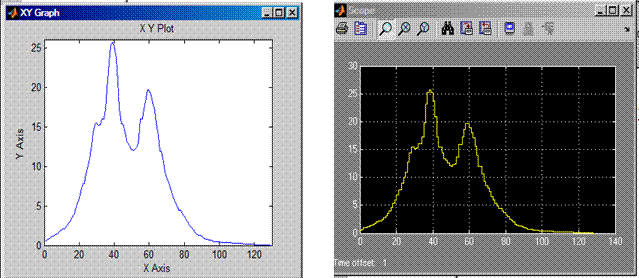
Рис.6.3. Полученные графики Simulink – модель специализированного процессора обработки сигналов на основе кубических базисных сплайнов.

Контрольные вопросы:

1. Что такое сплайн?

2. Что называется степенью сплайна?

3. Что называется дефектом сплайна?

4. Что такой специализированный процессор?

5. Объясните вычислительную структуру реализации аппроксимации функций кубическими базисными сплайнами.

6. Опишите модель спецпроцессора восстановления сигналов на основе кубических базисных сплайнов.

7. Какие блоки Simulink были использованы для реализации данной модели?

Литература:

1. Указ Президента Республики Узбекистан « О дальнейшем развитии компьютеризации и внедрении информационно-коммуникационных технологий».// «Народное слово», 2002 г., 1-июня.

2. Постановление Кабинета Министров Республики Узбекистан «О дальнейшем развитии компьютеризации и внедрении информационно- коммуникационных технологий».// «Народное слово», 2002 г., 8-июня.

3. Мякишев Д.В. Проектирование систем автоматизированной обработки данных: архитектура и базовые средства: Учеб. пособие. - Пенза: Изд-во ПГТУ, 1995.

4. Буч Г. Объектно-ориентированное проектирование с примерами применения: Пер. с англ. - М.: Конкорд, 1992.

5. Общесистемное проектирование АСУ реального времени: Под ред. В.А. Шабалина. - М.: Радио и связь, 1984.

6. Дьяконов В.П., Абраменкова И.В. Matlab 5.0/5.3. М.: Нолидж, 1999, 640 с.

7. Гультяев А.К. Matlab 5.2. Имитационное моделирование в среде Windows. СПб: Корона, 1999, 288 с.

8. Продеус А.Н., Родінова М.В. Безпаперова технологія проведення практикумів із статистичної обробки сигналів. – Электроника и связь, №20, 2003, pp.117-120

9. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. – М.,С-Пб,К., изд.дом «Вильямс», 2003. – 1092 с.

10. Калюжний О.Я. Моделювання систем передачі сигналів в обчислювальному середовищі MATLAB-Simulink. – К., “Політехніка”, 2004. – 135 с.

11. Дьяконов В. П. Simulink 5/6/7: Самоучитель. – М.: ДМК_Пресс, 2008. – 784 с.: ил.

Методические указания к

Выполнению лабораторных

работ по курсу «Проектирование

систем реального времени»

Рассмотрены и рекомендованы

к изданию на заседании

научно-методического

Совета ТУИТ

от « 19 » __января__ 2012 г

Протокол № 46

Составители:

Зайнидинов Хакимжан Насиридинович, д.т.н., профессор

Жовлиев Санжар Аролович, исследователь-соискатель

Отто Светлана Эрнстовна, магистрант гр. 204-11

Ответственный редактор: Зайнидинов Х.Н.

Корректор: Жовлиев С.А.